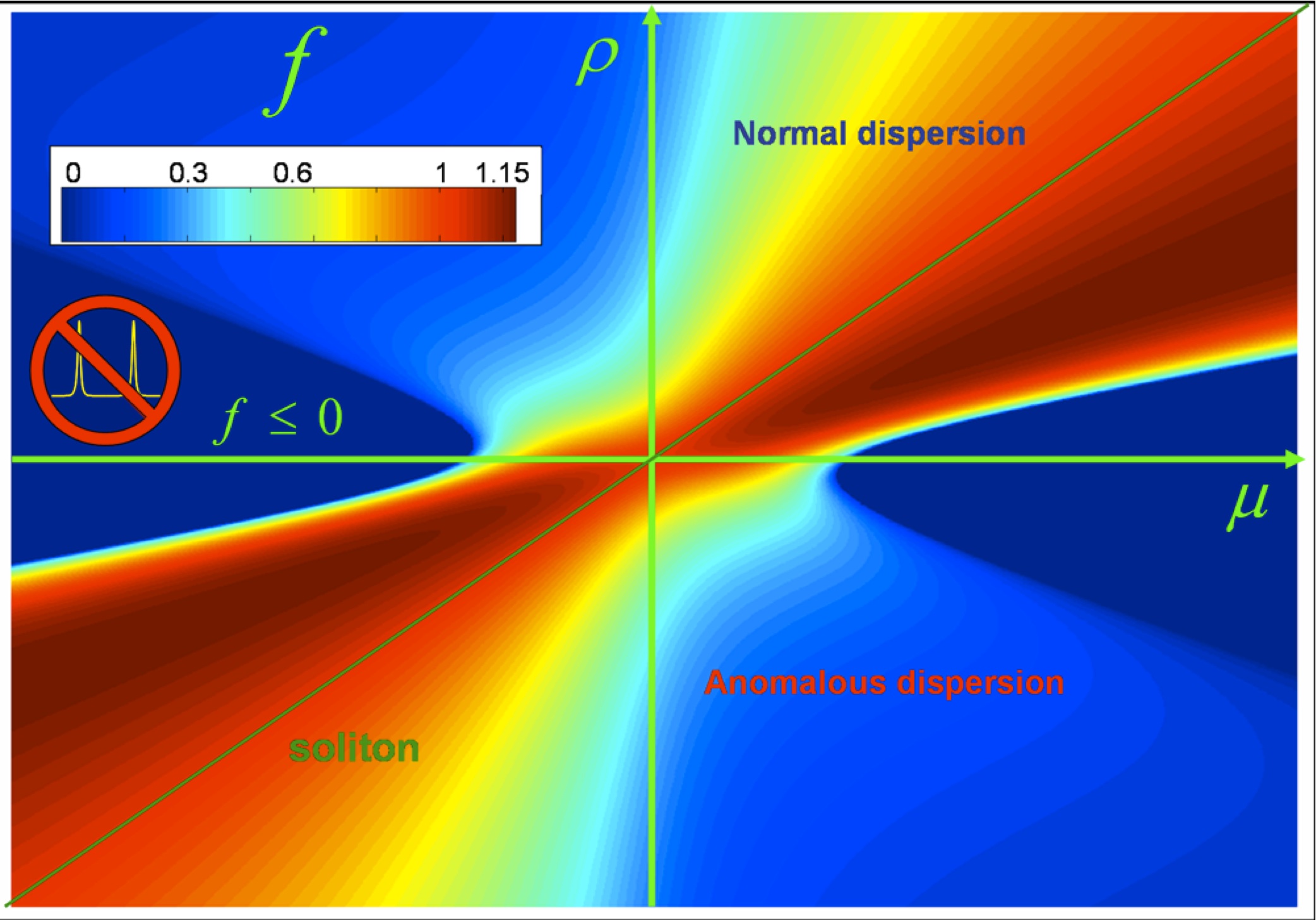
The combination of light-mode interaction and cavity noise in mode locked lasers gives rise to a rich phase diagram of nonequilibrium thermodynamics and statistical physics of light.

The competition between the ordering action of the saturable absorber and the disordering noise governs the creation of ultrashort pulses in a passively mode locked lasers, that is first-order phase transition from a high-entropy continuous wave steady state to an ordered mode locked state with a noisy continuum background.

The gain balance principle governs the distribution of the available power between pulses and continuum that experience the same gain, and yields the nonequilibrium passive mode locking phase diagram.

The self-starting of passive mode locking entails a noise-activated crossing of an entropic barrier and therefore a Poissonian distribution of the self-start time.

The injection of an external pulse train is the photonic analog of an external driving field, like pressure in statistical mechanics, and a strong injection causes the phase transition curve to terminate in a critical point. Exact mean field theory is valid, and the critical phenomena are captured by classical critical exponents.

Strong pumping that saturates the nonlinear absorber causes pulse breakup in a series of phase transitions to multipulse mode locked phases. Pulse powers are clamped, and pumping serves to increase the continuum power between sharp drops at pulse creation events.

Light modes dynamics in actively mode locked lasers is similar to non-interacting bosons in a one-dimensional trap potential given by the temporal gain profile. Standard, smooth gain modulation is equivalent to a harmonic boson trap, and therefore no Bose-Einstein condensation, and no mode locking transition. However, singular gain modulations allow for light-mode condensation, and consequent dramatic improvements in actively mode locked pulse properties.

The pulse fluctuations in a mode locked state are generated both by direct noise action and by interaction with the continuum. The latter increases the phase diffusion and makes the fluctuations non-Markovian with oscillating correlation functions.

The periodic scattering of the pulse off the discrete constituents of the laser cavity is a source of dispersive radiation that builds at discrete resonant frequencies, forming sharp Kelly-Gordon sidebands in the pulse spectrum. The cavity losses impart a finite spectral width to the sidebands, in contrast with the dispersive waves in free propagation that build up indefinitely. A gain-balance analysis of the multipulse mode locked state shows that the power of the sidebands increases with the pumping, and that they become narrower between pulse creation events.

It is widely observed experimentally that pulses in multipulse mode locked states interact, often forming tight pulse-bunch 'molecules'. An interaction mechanism based on gain depletion and pulse-continuum interactions explains the observations. The strong pulse create a gain shadow where the local continuum power is suppressed. The inhomogoneity in the continuum power biases the pulse fluctuations, and the drift creates an effective long-range pulse attraction. The further gain depletion by the dispersive-wave pedestals of the pulses generates a short-range repulsion. The theory predicts strong correlation between the steady state inter-pulse distances and the pedestal width that is confirmed experimentally.

The coherent light generated by multimode lasers can be compressed into extraordinarily short pulses when the phases of the lasing modes are aligned. These pulses, where light is comressed into a high intensity short signal, are used in a wide range of applications ranging from extreme precision metrology to optical communications networks. The mode locking is caused by a phase-ordering action—a saturable absorber in the case of passive mode locking—that renders the cw (continuous wave) operation unstable. However, the laser light is also subject to noise sources, most notably the intrinsic quantum noise generated by the optical amplifier. The noise introduces entropy into the many mode dynamical system, a disrodering agent which inhibits the formation of pulses. The competition between noise, that acts like temperature, and interaction between the many light-modes, means that the onset of mode locking is a nonequlibrium thermodynamic phase transition.

The mode locking phase transition is reminiscent of a ferromagnetic one when the complex mode amplitudes are viewed as vectors in two dimensions, as in the following sketch.

The left drawing shows the 'hot' cw phase, with disordered mode amplitudes, and the right drawing shows the 'cold' mode-locked phase, with mode amplitudes that undergo small fluctuations around a fixed alignment

The ordered, mode locked, phase corresponds in real time to an ultrashort pulse superimposed on a noise-driven cw. Simulation results demonstrate this result:

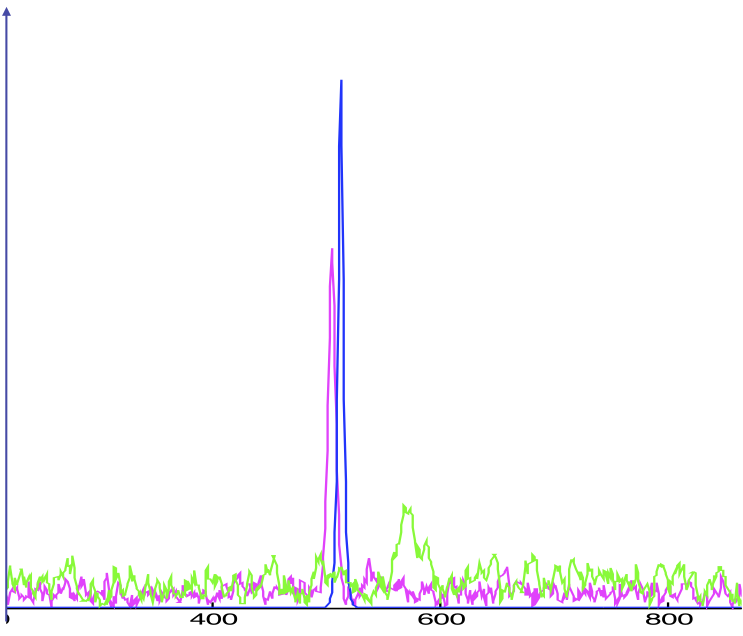
The green curve is a snapshot of the strong noise-high temperature state, pure cw; the blue curve is a snapshot of the no noise-zero temperature state, pure pulse; and the violet curve is a snapshot of the weak noise-low temperature state, with pulse and cw coexisting. The thermodynamics is much like that of a high density phase, liquid for example, with low potential energy but low entropy, coexisting with the low-density phase, like gas, that has high potential energy and high entropy, below the boiling point. The pulse and cw correspond to the liquid and vapor, respectively

The large scale separation between the short and intense pulse and broad and weak continuum validates a mean field theory that neglects the overlap between the pulse and continuum waveform, except insofar that they share the same gain and amplifier power budget. We developed two formulations of this principle. In the first the problem is mapped to a reference equilibrium problem, an effective free energy is calculated, and its global minimum is identified as the thermodynamically stable steady state, while local minima correspond to meta-stable states. This analysis showed that passive mode locking is a first-order phase transition. The cw phase always exists as a meta-stable state, but beyond an explicitly calculable threshold pumping level the thermodynamically stable state is mode locked, with pulse coexisiting with continuum. In particular this result resolved the long-standing self-starting problem.

The disadvantage of the equilibrium-mapping method is its limited applicability. It is valid only when the steady-state probability distribution is Gibbs-like; this can happen either by assuming the soliton condition, that serves as the potential condition for this system, or by an deriving an effective equation for the pulse power. The gain balance method does not rely on any assumption regarding the steady state distribution, and is therefore applicable to all systems. This method one identifies steady states with a consistent sharing of power between the different waveform components—pulse, continuum, and others. The stability tested by the gain balance analysis is local, so that it cannot distingusih the stabe from the meta-stable steady state. On the other hand, the meta-stable states are very long-lived, so that practically the question of global stability is less important than in traditional thermodynamics.

Passive mode locking works by applying more net gain to strong pulses that saturate a nonlinear absorber. However, this effect can only last up to a maximum peak power, beyond which the cavity transmissivity begins to decrease. When the peak power of a pulse surpasses this maximum, further pumping does not increase the pulse power, but may instead cause the formation of a second pulse in the cavity. This is in effect another first order phase transition. Further increase in pumping results in a cascade of transitions between ordered phases labeled by the number of pulses; these phase transitions are similar structural transition between phases of different order in solids.

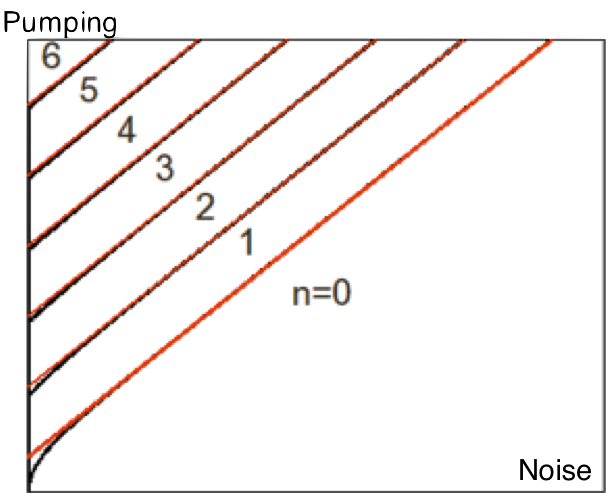
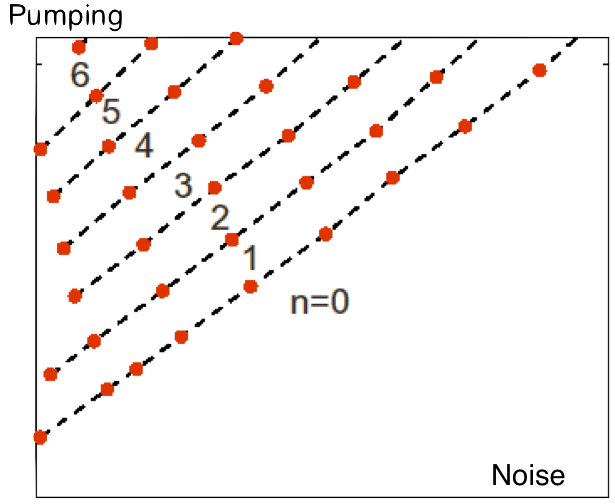
These are the calulated (left) and measured (right) multipulse mode locking phase diagram. n stands for the number of pulses, and n = 0 signifies the pure cw state. The left-most area of the theoretical phase diagram is not accessible in experiments becuase of the intrinsic noise. In the strong pumping, where the total power significantly exceeds the absorber saturation level, the phase transition curves are straight lines, and the pulse amplitudes tend to a fixed value. Increased pumping between phase transition leads to growth of the continuum waveform and of the Kelly sidebands.

When a pulse creation phase transition occurs, the new pulse arises from a randomly placed seed. However, the pulse location does not stay random—it moves slowly, typically approaching existing pulses to create a stable pulse bunch. The pulse parameters fluctuate because of the overlap of the pulses and the continuum. The continuum profile is not uniform:

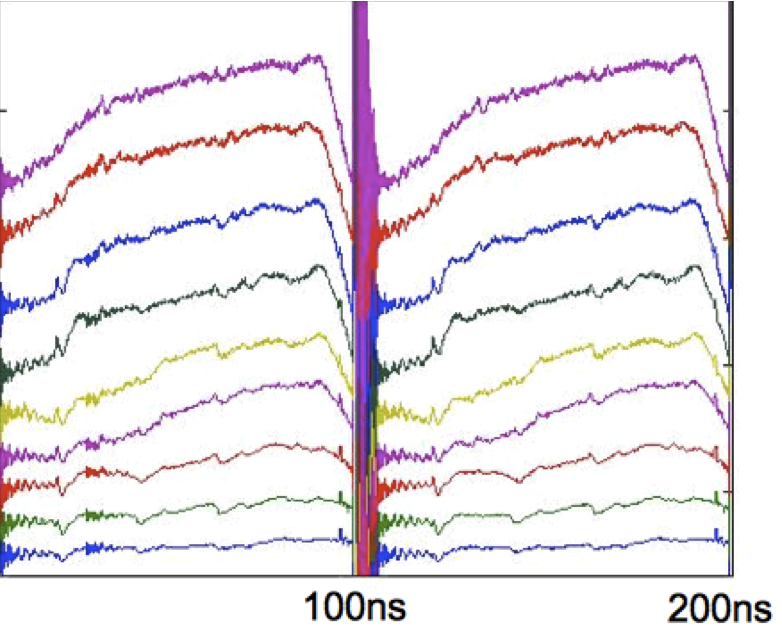
Shown are the two roundtrips of measured (left) and calculated (right) continuum waveforms for increasing pumping levels from bottom to top. The large signal in the middle of the experimental snapshot is the pulse bunch that is omitted from the theoretical graph. The pulses saturate the amplifier gain and leave a gain shadow with a weaker continuum intesnsity that slow increases as the gain recovers. The effect is stronger for stronger pumping.

The inhomogeneity in the continuum induces bias into the pulse fluctuations. The bias manifests as a drift toward the regime of larger fluctuations, causing an effective attraction that shares some of the properties of the Casimir effect in quantum electrodynamics. The dispersive waves that are observed spectrally as Kelly sidebands generate a pedestal that serves as the effective width of the pulses, where the attraction is replaced by repulsion, leading to the formation of pulse bunches.

Active mode locking is achieved by a temportal modulation of the gain. Unlike passive mode locking, it is a linear process, and pulses are formed at the point(s) of maximum gain. The simplest gain modulation is sinusoidial in the fundamental frequency of the cavity, that induces an ordering interaction between neighboring axial modes, quite similar to that of the ferromagnetic XY chain in the theory of magnetism.

The thermodynamics of active mode locking is therefore analogous to that if the ferromagnetic XY chain, that by the Landau argument does not undergo phase transition at any finite temperature for nearest neighbor interactions. Therefore, when the gain modulation is sinusoidal, full mode locking does not occur—rather, there are finite domains of locked modes that are not correlated between them. The defects in the axial mode represention translate to degraded pulse properties in the temporal waveform, they are both significantly longer and less coherent than the ideal noiseless pulses.

An altenative understanding of this phenomenon is obtained by representing the waveform in the normal modes of the cavity, taking into account the variable gain. When noise is disregarded all the cavity power resides in the lowest 'ground state' mode, but the noise cause occupation of many 'excited state' normal modes with random phaes that broaden the pulse and degrade its coherence properties. It turns our that there is a close connection between the power distribution of the normal mode, and the occupation statistics of noninteracting boson in an external potential whose shape is given by the gain modulation profile. As pointed out by Einstein, noninteracting bosons condense into a macroscopic occupation of the ground state below a transition temperature. However, condensation occurs only for high enough dimensionality: Free bosons condense in dimensional larger than two, and bosons in a harmonic trap, that corresponds to sinusoidal gain modulations condense only in more than dimension. The occupation of the ground state is never macroscopic, and no sharp transition to mode locking occurs.

However, condensation can be achieved in one dimension, if the gain modulation (or external potential in the case of noninteracting bosons) is singular, with a power law maximum. Then there is a threshold pumping level, above which power starts to accumulate in the ground state mode:

These graphs show the calculated power in the ground state mode as a fraction of total cavity power. η is the exponent characterizing the gain profile at the minimum, so that η = 2 corresponds to a smooth modulation that does not allow for condensation, while η = 1 corresponds to a singular gain modulation that allows condensation, manifest as a sharp rise in fundamental mode power. The transition becomes sharper as the number N of active modes increases.

Experimentally, condensation is observed as a sharp narrowing of the actively mode locked pulse accompanied by a dramatic reduction in the noise level

as seen in the three bottom-right of these experimental snapshots taken with different values of the exponent η and of the pumping increases from top to bottom.