Quantum optics and cold-atom dynamics in the semiclassical limit

Phase-space dynamics lends an exact classical probabilistic underpinning to a harmonic oscillator if the initial state has a positive Wigner function, but this underpinning is only approximate for nonlinear oscillators. The breakdown of the classical underpinning is quantified by the leading nonclassical phase-space dynamics in the Heisenberg picture.
In contrast, successive measurements of a quantum system can cause breakdown of macroscopic realism even in a harmonic oscillator prepared in a positive-Wigner-function state. The breakdown of macrorealism is demonstrated by large violations of the Leggett-Garg inequality for measurements of a squeezed action observable, that can be implemented experimentally with an entangled photon pair.
The atomic polarization in the Jaynes-Cummings model of cavity quantum electrodynamics (CQED) exhibits collapse and revival of Rabi oscillations for a coherent state prepation of the cavity mode. A Heisenberg-picture analysis of the cavity mode phase-space dynamics with an atomic internal degree of freedom reveals post-classical Rabi oscillations for a trapping atomic prepatation as well as small-amplitude field Rabi oscillations.
The cavity electromagnetic field in CQED becomes entangled with a resonantly interacting atom, and this entanglement can in turn be transferred to a second atom to create an entangled photon pair. A coherent field state is normally considered to become classical for large photon number. Nevertheless, atoms can be entangled through interaction with a field mode prepared in a coherent state with an arbitrarily large number of photons, with 20% of maximal entanglement in the classical limit. The same effect is achieved when the cavity modes interacts with two atoms simultaneously.
Reversing the role of field and atom, two electromagnetic cavity modes become entangled when coupled resonantly to a common 2-level system. An initial product-coherent-state field preparation splits in phase space, and after the decoupling of the 2-level system, the field-field state becomes a Bell state of two nearly orthogonal wavepackets, in spirit a Bell state compose of entangled Schrödinger cats
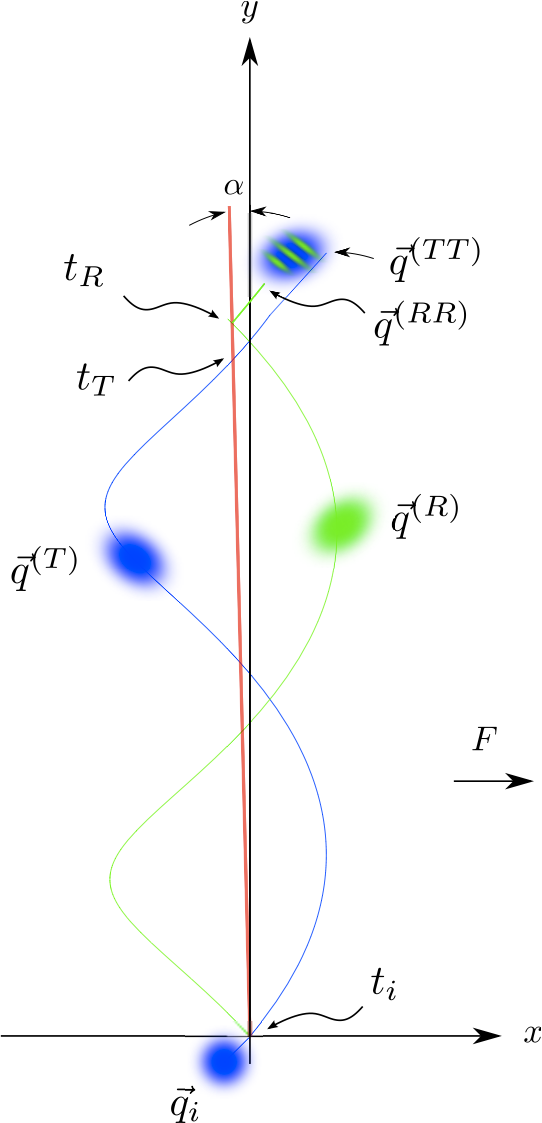
A cold-atom wavepacket undergoing Bloch oscillations under the combined influence of an optical lattice and an external forcing accumulates a dynamical phase. The phase can be detected using a cold-atom beam splitter that acts as a Mach-Zehnder interferometer. The interferometer is a highly sensitive probe of the optical-lattice band structure, and can directly measure the associated Berry phase when the lattice breaks space inversion symmetry.
Background
The semiclassical approximation is useful in quantum systems where the typical action scale is much larger than Planck's constant. Then the dynamics of observables in the Heisenberg picture and states in the Schröridenger picture can be approximately captured by classical dynamics. For this purpose it is beneficial to represent the observables and states in phase space, usually using the Weyl representation, where states are represented by their Wigner functions. It can then be shown that smooth quantum observables, such as position, momentum and energy evolve approximately like classical observables, and semiclassical states, that can be either wavepackets localized at a phase-space point, or WKB states localized on Lagrangian manifolds, evolve approximately like classical phase-space densities. These results can be regarded as examples of the correspondence principle that states that classical physics should be recovered from quantum physics in the limit of large quantum numbers.
Many interesting phenomena occur in composite systems where only some of the degrees of freedom are semiclassical. Semiclassical ideas and methods are useful in studying such systems. The reference classical dynamics in such mixed quantum-semiclassical systems is non-standard, with matrix- or operator-valued Hamiltonians. As a consequence, quantum corrections to the Hamiltonian arise&mdashthe Berry term that generates the Berry geometric phase, and the non-geometric but gauge-invariant Wilkinson-Rammal term. An example of a mixed system is that of a charge under the combined influence of a magnetic field and a periodic potential in two dimensions, that yields the famous Hofstadter butterfly. If the magnetic flux through a unit cell of the potential lattice is close to rational, the deviation from rational serves as a semiclassical parameter. The magnetic sub-bands energies then obey the Bohr-Sommerfeld quantization rules for a one-degree of freedom Hamiltonian that is periodic in momentum as well as in position, and the Berry and Wilkinson_Rammal phases appear as Maslov-index like quantum corrections for the classical action in the quantization rule.
Semiclassical-field-mediated entanglement in cavity quantum electrodynamics
Cavity quantum electrodynamics (CQED) describes the coherent interaction of few-level systems and discrete electromagnetic modes in high-Q cavities. Experimental systems were first realized by coupling atoms or ions to resnonant electromagnetic cavities, either in the optical or the microwave. More recently similar effects have been achieved in superconducting circuits, where resonant circuits based on Josephson junctions take the role of the atoms, and the electromagnetic modes are realized with microwave transmission lines.
In the strong-coupling regime, where the atom-field interaction is stronger than the dissipative and dephasing processes, CQED explores the fundamental properties and processes of quantum mechanics. For example, an entangled pair of atoms in a Bell state was produced in 1997 by the Paris group. In that experiment the cavity was prepared in the ground (vacuum) state, and served as a quantum gate.
CQED can also be used to probe the classical limit and the correspondence principle, when a cavity mode is excited to a high-photon number state. It is a mixed quantum-semiclassical system, becuase the atoms never become classical. In the simplest case a single two-level atom interacts with a single mode prepared in a coherent state. The field-atom interaction generates fast Rabi oscillations of the atomic state and a slow dynamics in the field phase, that causes the field state to split into a superposition of two wave packet that are well-separated in phase space.—a photon "Schrödinger cat."
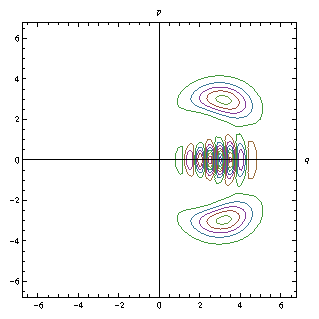

In our work we examine the dynamics of a cavity mode in a coherent state preparation coupled to two two-level atoms, to test whether highly-excited, semiclassical field mode can serve as an entanglement agent in the same way that a vacuum field does. The interaction with the two atoms can be either sequential or concurrent: in both cases the field wave packet splits into three pieces:

The middle wave packet, that is a coherent state, is tensor multiplied with an entangled 2-atom state, while the two flank wavepackets are tensor multiplied with separable 2-atom states. The 2-atom reduced density matrix is obtained by tracing over the field degree of freedom that yields a mixed 2-atom state.
Our purpose is to study the entanglement properties of the 2-atom state. Unfortunately, there exist inequivalent entanglement monotones for mixed systems, and this means there is no unique measure of entanglement for them.
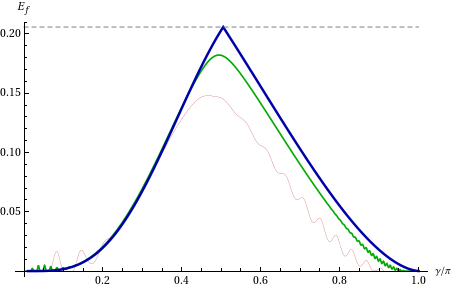
Shown is the entanglement of formation of the 2-atom mixed, that is the mean number of maximally entangled pairs required to distill the state, as a function of the phase space angle γ swept by the wavepacket fragments during their interaction with each atom. The red and green curves correspond to numerical calculations with finite mean number of photons and the blue curve corresponds to the limit where the average number of photons is taken to infinity. The maximum at γ=π/4 is a consequence on an interesting trade off. The pure 2-atom entangled state associated with the center wave packet is (almost) maximally entangled for small γ, but it is orthogonal to the two flank wave packet atomic states, so that the resulting mixed state is separable. As γ increases, the degree of entanglement of the center state decreases, but its overlap with the flank atomic states increases, so that the degree of entanglement first increases, then drops to 0 for γ=π/2.
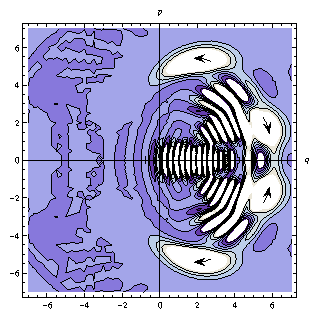
Contour plot animations (top) and 3D animations (bottom) showing the full dynamics of the field's Wigner function in phase space. These correspond to a sequential interaction of the field with the two atoms.
The wave packet dynamics and entanglement generation discussed so far are valid in the limit of large photon numbers. Evidently, a semiclassical field state can mediate quantum interaction between two two-level systems and entangle them. The degree of entanglement achieved is not maximal, but is finite in the semiclassical limit. This seems to contradict the correspondence principle according to which classical physics should be recovered in the limit of large quantum numbers, and classical physics has no concept of entanglement. However, the entanglement is obtained for a fixed value of γ, and the dynamics in phase space is slower the higher the photon number, so that the time needed to entangle the atoms diverges in the classical limit. This is a manifestation of the fact that the semiclassical limit is singular and the limits of large quantum numbers and long times do not commute.
Entanglement of two semiclassical electromagnetic cavity modes
Two modes of the electromagnetic field can interact with each other indirectly through their simultaneous interaction with a mediating qubit. We show how this effective mode-mode interaction can generate entangled two-mode states, such as two-mode squeezed states and N00N states, using experimentally feasible superconducting circuits.
In our work both field modes are prepared in semiclassical coherent states with large average photon numbers. The interaction with the qubit causes the initial product to evolve into a superposition of two two-mode squeezed states. The two-mode Wigner function lives in a 4-dimensional phase space, and the single mode Wigner function is its 2-dimensional projection,
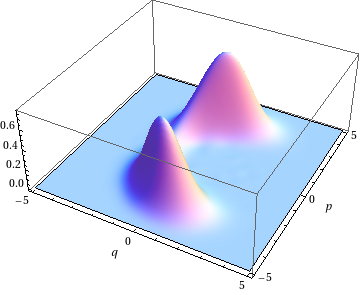
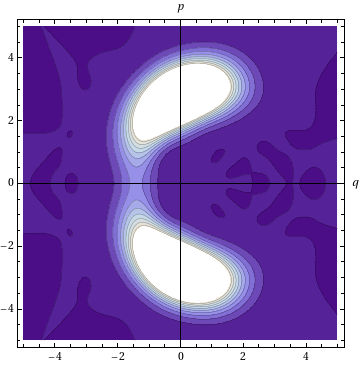
shown at one of the special instants where the field and qubit decouple. The final two-mode state is a superposition of two states localized in the four-dimensional phase space, so that it's a CQED version of entangled Schrödinger cats that are simultaneous both dead and both alive, but a measuement verifying that either is alive, say, implies that the other is also alive.
The two-mode entanglement implies Bell inequality violation. Like 2-qubit Bell inequality violation, the expectation value of the Bell opertor depends on a tilt angle φ, and local realism implies that the Bell expectation is less than or equal to 2.

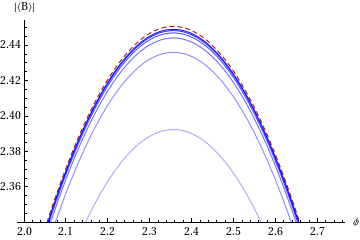
On the left panel the expectation of the Bell operator as a function of φ is shown in blue and compared with the green curve that shows Bell expectation for a superposition of products of squeezed coherent states. The green curve saturates the Cirel'son inequality, but the actual two-mode states does not, because it carries a second type of entanglement, two mode squeezing, and the two types of entanglement are mutually competetive. The right panel shows the Bell expectation for variable the average photons number of the modes, increasing from bottom to top. Two-mode entanglement is demonstrated in the classical limit of large photon number (red dashed curve); as in the two-qubit entanglement, the correspondence principle is upheld because the interactio time diverges in the classical limit.