Research Interests

Field theory combined with AI

Condensed matter physics studies the collective behavior of interacting many-body systems. As tracking all degrees of freedom in such settings is futile, both analytical and numerical progress hinges on identifying the most relevant collective degrees of freedom for any given problem. In simple settings the latter are just local averages of microscopic quantities such as particle velocities, charge, or spin. For some systems the relevant degree is far less obvious, for instance the quantum phase of the cooper pairs in super-conductors. For phenomena at the forefront of this field, a clear understanding of relevant degrees of freedom is either lacking or incomplete. Such is the case for various gauge theories, quasi-periodic systems, disordered systems, and out of equilibrium systems.

Phrased as above condensed matter systems clearly invite the use of big-data methods, where identifying the relevant features based on which inference can be made, is also considered a primary task. The use of big-data methods, namely deep learning, has already proved practical in quantum chemistry a nearby research field. However like most deep learning algorithms, it is difficult to gain intuition or analytical insight from the inner-workings of such huge and complex inference models.

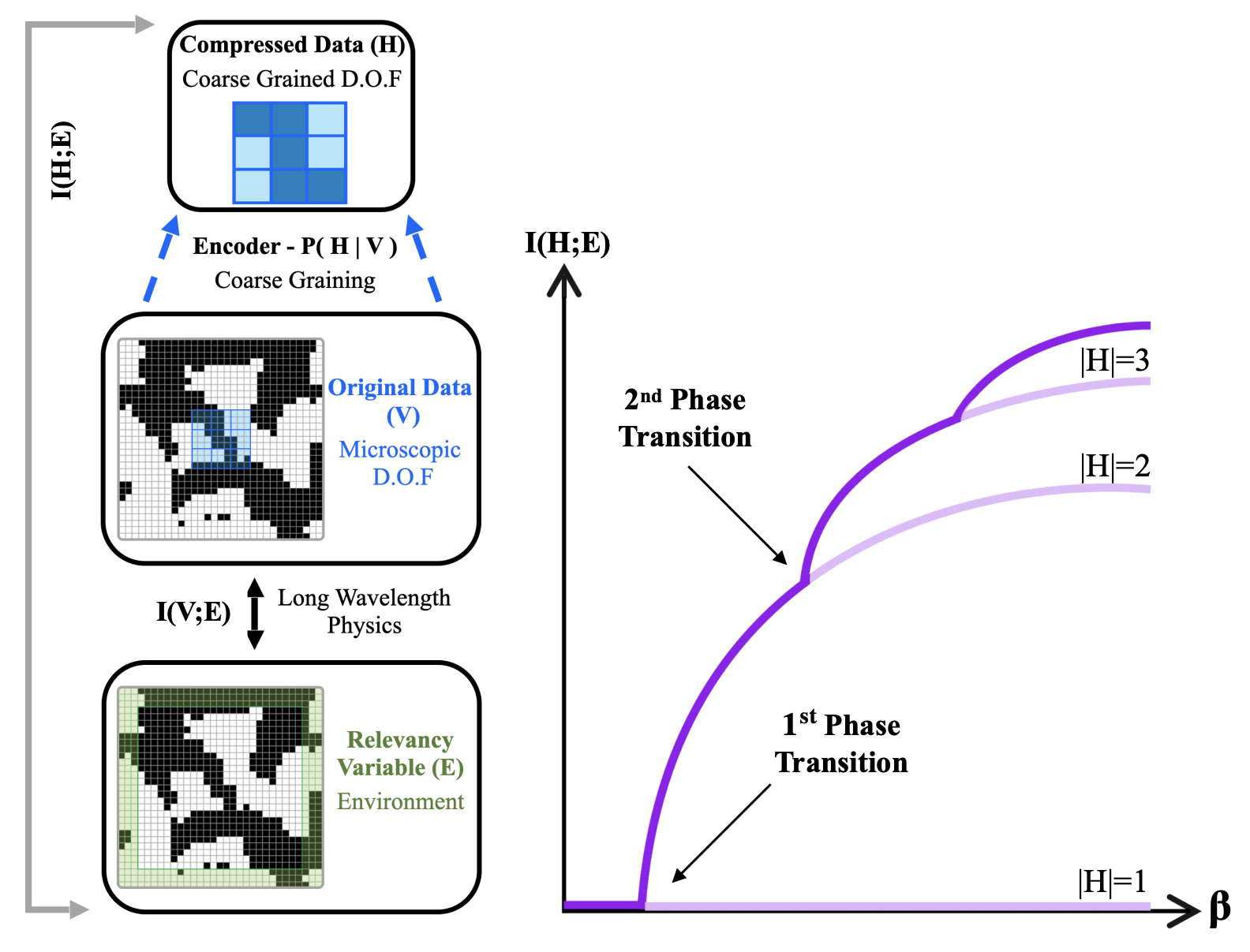
To combine the feature learning capabilities of deep learning with the theoretically appealing formalism of condensed matter physics, we use a hybrid approach to analyze complex systems. We learn the most relevant degrees of freedom on a local scale and then use field theory tools, in particular the renormalization group formalism, to track and intepert these degrees of freedom in a sensible field theory manner. Central to our approach is the use of information theory as a common ground between field theory and deep learning. Our first goal to expedite the discovery of novel field theories and novel mechanisms for collective behavior in an analytically trasparent manner. Our second is a proof of concept that deep learning can and should be integrated into the work-flow of condensed matter physics.

Deep learning and physics

The recent increase in availability of big data and powerful computers is gradually altering the way we program. Instead of carefully crafting algorithms with a clear logical structure and execution flow, tomorrow's programmer is more likely to train a general purpose artificial neural network to solve the problem they are tackling. Notably the innards of an artificial neural network bear more resemblance to an artificial material than to a computer algorithm. Thus, they become amenable to various analysis techniques unique to condensed matter physics. Indeed, debugging an artificial neural network or assessing its capacity for information processing is becoming more and more like a task in material engineering than in programming. While the technical know-how in this field is accumulating fast, the theory behind artificial neural networks, especially deep neural network, is still in its infancy.

This is fascinating to explore, and not solely for computational reasons. This new context also makes us ask very different questions about the artificial materials we use to represent the neural network. Instead of the typical experimental questions one asks in real materials, concerning their resistivity or elasticity, here the focus turns to questions about information and sensitivity. Thus such theoretical explorations may help us build better machine learning algorithms while improving our understanding of the curious interdependencies between physics, information, and computational complexity.

Complexity aspects of physics

It has been understood from early on that simulating quantum physics is fundementally hard. One of the most remarkable advancements in fudemental physics in the past 30 years was Shor's algorithm which showed that quantum mechanics is not just hard to simulate--- it is in fact a stroger computational model which is, according to standard complexity assumptions, distinct from any classical computational model. Alternatively stated no classical computer can simulate all quantum phenomena while a (still putative) quantum computer can simulate all classical phenomena. In addition it could solve some computer-science problems which are believed to be insolvable using a classical computer in reasonable time.

Notwithstanding, to date, no remarkable quantum speedup of any useful classical algorithm has been demonstrated. Some believe these are just technical setbacks while others conjecture that there may be fundemental problems in making quantum mechanics do large scale computations.

Focusing on condensed matter physics, the natural computational problem which arises is how to compute equilibrium and dynamical properties of many-body systems consisting of either electrons of spins. Various clever algorithms has been devised to tackle this hard problem in particular Tensor-product-states, quantum Monte-Carlo, and density functional theory. I am interested in finding ways of imporving these techniques as well as proving that some problems in condensed matter are intracatble using these algorithms. Furthermore I'm interested in hybrid computational schemes where some portion of the computation is done on a limited quantum hardware.

Topological phases of matter

The sum being greater than its parts is a common theme in condensed matter physics. Systems made of a large amounts of simple constituents often exhibit intriguing collective phenomena. The fractional Quantum Hall effect (FQHE), in which electrons may fractionalize into quark-like particles, and superconductivity, where electrons flow with zero resistivity are just two examples of out of many. Of course such emergence of complex structures is by no means limited to physics--- Biology emerges from chemistry and intelligence emerges, arguably, from many coupled neurons. What distinguishes the condensed matter context is that occasionally, after much hard work, and using advanced tools such as field theory and algebraic topology--- we can gain an analytical understanding and make accurate predictions of emergent phenomena which arise in realistic complex systems.

Much of the exotic collective phenomena which we understand best lays within the field of topological phases of matter. This broad field consists of many interesting systems which include the above FQHE as well as systems made of quantum spins, classical spins, photons, phonons, and mechanical devices. In fact new theoretical models and experimental realizations are been discovered on a yearly basis driven partially by the promise of topologically protected qubits and fault tolerant quantum computation. Classifying the various types of topological phases, understanding their computational capacities, and identifying real materials which realize them are some of the important challenges in this field.