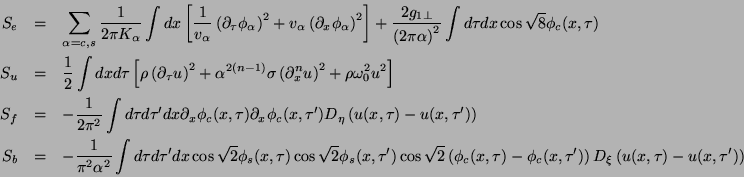
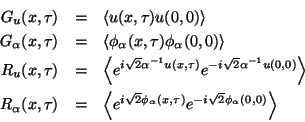
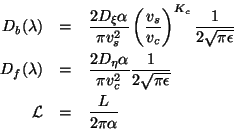
![]() and
and ![]() are dimensionless parameters associated
with the string
are dimensionless parameters associated
with the string
| realization | ||||
| Rigid String |
|
|
 |
|
| Flactuating String |
|
|
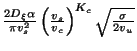 |
|
| Very Floppy String |
|
|
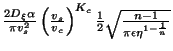 |
|
| Stationary String |
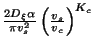 |
|
||
![\begin{eqnarray*}
G_{\alpha o}(x,\tau ) & = & -\frac{K_{\alpha }}{4}\ln \frac{x^...
...}-\left(\frac{v_{u}\tau }{\alpha }\right)^{1-\frac{1}{n}}\right]
\end{eqnarray*}](img26.png)
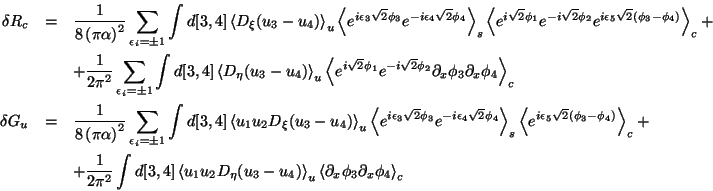
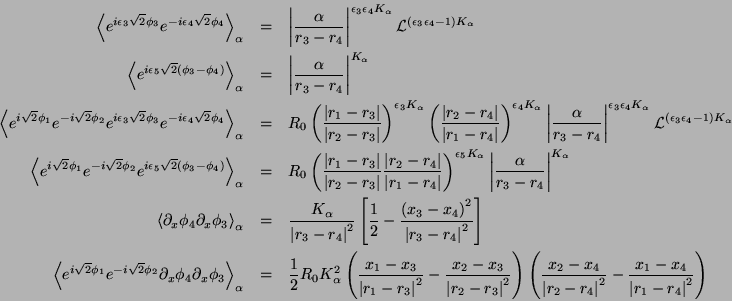
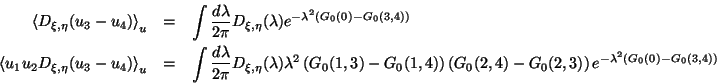
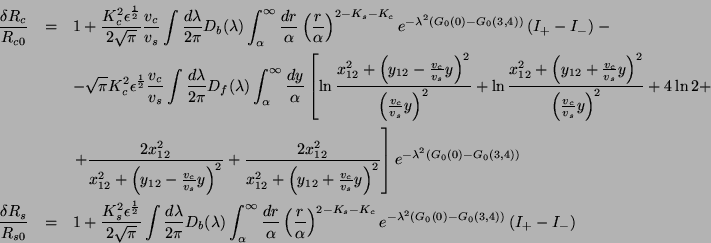
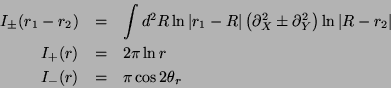
![\begin{eqnarray*}
\delta G_{u}(r) & = & 4\sqrt{\pi }\frac{\mathcal{L}}{\mathcal{...
...{\varpi }{\alpha }\left(\left\vert r\right\vert-x\right)}\right]
\end{eqnarray*}](img34.png)
with
![]()
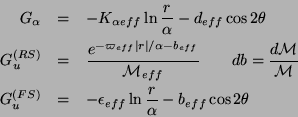
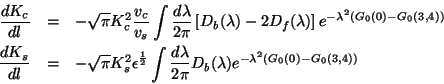

when ![]() is constant
is constant

Define
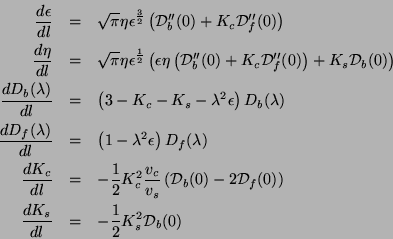
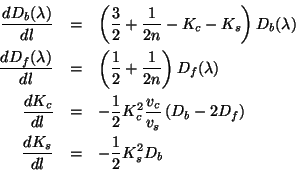
averaging over the string degreed of freedom,
![]() ,
and seperating elastic and inelastic terms
,
and seperating elastic and inelastic terms
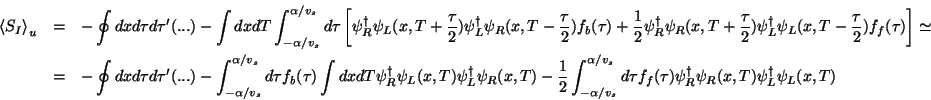
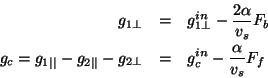
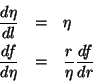
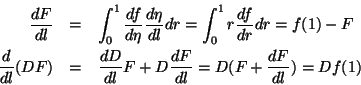
This document was generated using the LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 2 rgSummary2.tex
The translation was initiated by Uri London on 2005-01-12