This is a Penning-Malmberg trap for confinement of a pure electron plasma. The radial confinement is provided by axial magnetic field, while negatively biased end electrodes yield axial confinement. Initially, the electrons are injected from the filament and trapped afterwards by raising the potential of the end electrodes. Numerous experiments with these plasmas are performed by J. Fajans group at UC Berkeley. Autoresonant excitation of the diocotron mode is one of them.

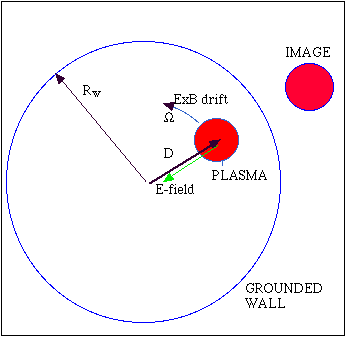The diocotron mode is a trapped pure electron plasma column performing azimuthal ExB rotation due to the radial electric field E of the positive image charge created when one grounds the confining cylindrical wall of the trap. One finds that the rotation frequency W of the mode is related to its amplitude D and wall radius R_w as W=W₀/[1-(D/R_w)²], where W₀ is proportional to plasma density and gives the diocotron frequency at D=0. Assume that, initially, the plasma column is at D=0. Then, by inserting an additional driving electrode into the trap and oscillating its potential at slowly increasing frequency w(t) and passing the resonance w=W₀ one can enter autoresonant evolution stage. In autoresonance, the mode amplitude D grows to stay in the continuing nonlinear resonance w(t)=W(D(t)) as the driving frequency increases in time. Typical experimental data on excitation of the mode is shown below.

    Figure (a) illustrates the growing mode amplitude beyond the linear resonance (at t=0.0015s). The autoresonance is destroyed after the plasma reaches the wall at t=0.00375s.
    Figure (b) shows the phase difference between the driving potential and the rotating plasma. The phase locking in autoresonance (0.0015s<t<0.00375) is seen in the figure.
    Figure (c) proves that only a single linearly increasing frequency is present in the output signal from the plasma in autoresonance (time interval (0.0015s<t<0.00375). The plasma is simply phase locked to the drive.

    IMPORTANTLY, for entering autoresonance by linearly chirping the driving frequency, one must satisfy the threshold condition on the driving amplitude e, i.e. e>e_th, where e_th~A^3/4, A being the chirp rate.