STUDENTS:
Master's and Ph.D. projects are available in a fascinating new theoretical research topic involving semi-classical dynamical systems. Contact me for more details.
Research
Areas:
Nonlinear dynamics and statistical physics of
ultrashort laser pulses
- The coherent light generated by multimode
lasers can be compressed into extraordinarily short pulses when the
phases of the lasing modes are aligned. These pulses, where light is
comressed into a high intensity short signal, are used in a wide range
of applications ranging from optical communications networks to probing
basic processes such as real time atomic dynamics. The formation
and evolution of the pulses is therefore an interesting and
important
area of nonlinear optics and nonlinear dynamics in general.
- However, the laser light is also subject to
noise sources, most notably the intrinsic quantum noise generated by
the optical amplifier. This noise introduces entropy into the
many mode dynamical system, a disrodering agent which inhibits the
formation of pulses.
-
-
 
|
Complex amplitudes of lasing modes in
continuous wave (cw) operation (left) and mode locked operation
(right). The switching
from cw to pulsed
operation is an ordering
phase transition, as in, for
example, the ordering of spins in a ferromagnet.
|
- The process of pulse formation is therefore the
consequence of stochastic
lightmode dynamics (SLD), i.e., many mode
dynamics subject to noise. The onset of mode locking iteslf has a
precise significance of a thermodynamic phase transition in a far from
equilibrium setting.
- An important method to achieve pulse formation
is
passive mode locking wherein one introduces into the the laser
cavity a saturable
absorber - a nonlinear passive element which becomes more transparent the higher
the intensity of the incident light. Labeling the absorber saturability
by
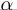 the intracavity power by P
and the noise power by T,
we have shown that when the dimensionless parameter
the intracavity power by P
and the noise power by T,
we have shown that when the dimensionless parameter  is increased, the light mode system experiences a first
order transition from a disordered cw phase, where the
invariant measure is concentrated on cw waveforms, to a mode locked
phase, where probable waveforms consist of a short pulse accompanied by
a weak cw background. Under certain circumstances the transition occurs
when
is increased, the light mode system experiences a first
order transition from a disordered cw phase, where the
invariant measure is concentrated on cw waveforms, to a mode locked
phase, where probable waveforms consist of a short pulse accompanied by
a weak cw background. Under certain circumstances the transition occurs
when  has the precise value 9. The results are
obtained using exact mean field theory. has the precise value 9. The results are
obtained using exact mean field theory.
-
-
  |
Typical laser cavity optical
waveforms in the cw phase (left) and mode locked phase (right). The
fluctuations are generated by the intracavity noise, and are
characterized by the
coherence length. Mode locking occurs when the pulse width
is shorter than the coherence length. Thus, the onset of mode locking
is an abrubt discontinuous process.
|
- The simple picture described above is valid
only when the pulse peak power is not too large. When the pulse power
is large eneough to saturate the absorber, the laser may reach a
situation where it is more favorable to form two or more pulse per roundtrip period.
Then the thermodynamics of the ligth mode system is described as a
cascade of first order phase transition in a phase diagram with many
phases, labeled by the number of pulses.
- Another twist is occurs when the mode locked laser is
coupled to an external source of pulses. The external pulse source
assumes the role of an extenral driving field in the theory of phase transitions. When the external seeding is strong enough, the cw-pulse transition disappears in a critical point. The critical point
is exactly described by the Wan der Waals theory of phase
transitions, and classsical exponents have been measured experimentally.
Geometric swimming and motion in
classical gauge
field
- Swimming is a form of self propulsion,
where
translational or rotational motion is achieved by a series of
deformations. When the swimming motion occurs in conditions of low
Reynolds numbers, that is, when inertia is completely negligible
compared to the viscous forces, then swimming is geometric. That is,
that the total motion depends only on the series of shapes achieved by
the swimmer and not on the rate of deformation. Since the Reynolds
number is proportional to the size and speed of the swimmer, swimming
of microscopoic objects, whether microorganisms, or microrobots is
geometric. A related problem,
which shares many of the propetries of geometric swimming, while being
easier to analyze, is the rotation withouit angular momentum of freely
suspended objects, as in
the famous ability of a falling cat to land always on its feet, again achieved by a series of deformations.
- Mathematically, geometric swimming is
described
using a connection on a fiber bundle, a concept better known in
physics as a gauge field.
The gauge field is defind on the space of all
possible shapes - in principle an infinite-dimensional space -
which can be reduced significantly by considering swimmers whose
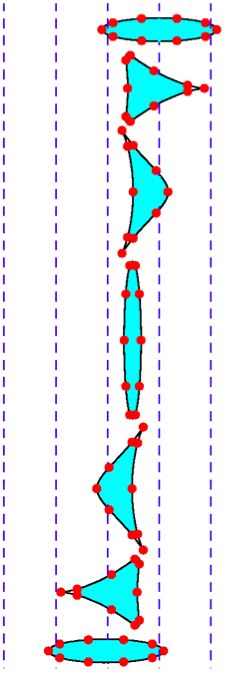
shapes are confined to a certain predefined class. For example, the
swimmer shapes shown in the adjacent figure are obtained as the image
of the unit circle under members of a certain two-parameter family of
conformal maps. As a consequence of its up-down symmetry, the depicted
two-dimensional swimmer can only move in the horizontal direction, and
cannot rotate. The swimming action can be described in physical terms
using a 'magnetic field' defined on the two-dimensional abstract shape
space. A swimming stroke can be defined as a closed orbit, i.e. a loop, in the
space of shapes, and the translation achieved by the swimmer is equal
to the 'magnetic flux' through the loop.
- The research work described here
focused on the question of efficiency. Namely,
we asked how the swimmer can perform a certain task, such as
propelling itself a given distance, using the minimum amount of energy. This
question is especially pertinent for artificial swimmers, which have to
work with a limited supply of energy. Since the dissipation of energy is
a quadratic functional of the swimmer path, the problem of identifying
the optimal swimmer is isomorphic to Hamilton's principle of least
action in the clasasical mechanics of a charge in magnetic field,
where the 'kinetic energy' is defined by a Riemannian
metric derived from the energy dissipation functional. The shapes shown
on the right are a series of snapshots from the solution of
the mechanical problem in a conveniently picked space of shapes. The
swimmer advances horizontally, and the snapshots are shifted vertically
only for visibility. The swimming stroke they describe is the most
energitically efficient one in the class of shapes studied.
|
|
|
 |
Fractal spectra and magnetic oscillations in
lattices threaded with a magnetic field
 - The
Harper-Hofstadter system is one of the
paradigms
of solid state physics. First cosidered by Peierls, it describes
non-interacting fermions hopping on a two-dimensional lattice and
subject to a transverse magnetic field. In the tight-binding
approximation the Hamiltonian is periodic in
the magnetic field, depending only on the magnetic flux threading a unit
lattice cell modulo the flux quantum h/2e The energy spectrum of the system has a very
unusual dependence on the magnetic field. When the number of flux quanta
is rational, Bloch's theorem applies, and the spectrum consists of a finite number of bands; when the number of quanta is
irrational, on the other hand, the spectrum is a Cantor set of zero
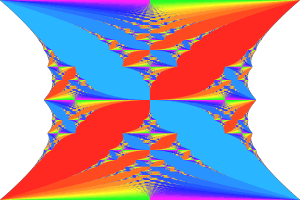
measure. When the spectrum of the Hamiltonian is plotted against the
strength of the magnetic field for several rational values, the
beautiful picture shown on the right emerges. It is nicknamed
'Hofstadter's butterfly'. In the figure shown, the gaps, which are of
full measure because of the fractal mature of the spectrum, are colored
by the associated value of the Hall conductance, which is integer and
constant in each gap, because of the quantum Hall effect.

- As a consequence of the extreme sensitivity of
the energy spectrum in the Hofstatdter system, physical quantities
which involve differentiation with respect to magnetic field are
strange and singular. This is indeed observed in the (orbital)
magnetizartion, the derivative of the free energy with respedct to the
magnetic field. At zero temperature the magnetiuzation in the gaps is
an
oscillating piecewise linear function of the Fermi energy, whose frequncy of oscillations
grows without bound when approaching a magnetic Bloch band, filling a
two-lobed envelope. The adjacent figure shows the magnetization
oscillations as a function of the Fermi energy when the magnetic flux
is close to one third. They are
the lattice analog of the well-known de Haas-van Alphen magnetic
oscillations predicted by Landau. The shape of the envelope reveals some subtle properties
of the quantum state, such as Berry's phase, and a second quantum phase
first discovered by Wilkinson, Belissard and Rammal.
|






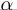 the intracavity power by
the intracavity power by  is increased, the light mode system experiences a first
order transition from a disordered cw phase, where the
invariant measure is concentrated on cw waveforms, to a mode locked
phase, where probable waveforms consist of a short pulse accompanied by
a weak cw background. Under certain circumstances the transition occurs
when
is increased, the light mode system experiences a first
order transition from a disordered cw phase, where the
invariant measure is concentrated on cw waveforms, to a mode locked
phase, where probable waveforms consist of a short pulse accompanied by
a weak cw background. Under certain circumstances the transition occurs
when  has the precise value 9. The results are
obtained using exact mean field theory.
has the precise value 9. The results are
obtained using exact mean field theory.

