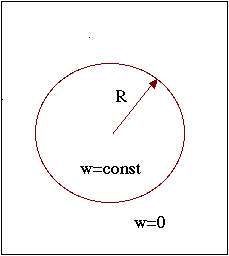
 Circular Vortex in Two Dimensional Fluid.
Circular Vortex in Two Dimensional Fluid.
Azimuthal Fluid Velocity Field: V(x,y,t)=V(r)ef
SHORT INTRODUCTION TO 2D VORTICES
 Circular Vortex in Two Dimensional Fluid.
Circular Vortex in Two Dimensional Fluid.
Azimuthal Fluid Velocity Field:
V(x,y,t)=V(r)ef
Vorticity: w=rot V=w(r)ez
Simplest vortex:
w=const, r<R
w=0, r>R
Stokes's law:
V=wr/2, r<R
V=wR/(2r), r>R
 Kirchhoff
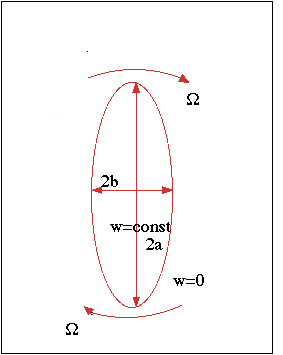
Elliptic Vortex is a generalization of a circular vortex.
Kirchhoff
Elliptic Vortex is a generalization of a circular vortex.
Kirchhoff Vortex has a constant elliptic shape (principal
axis a and b) and rotates with angular frequency
W=wab/(a+b)2=wr/(r+1)2,
r=a/b
Individual particles in the Kirchhoff vortex move on
off-axis circular trajectories with angular frequency 2W.
r(t)=(w/w)+[(w/w)2-2(w/w)]1/2-1
 THE
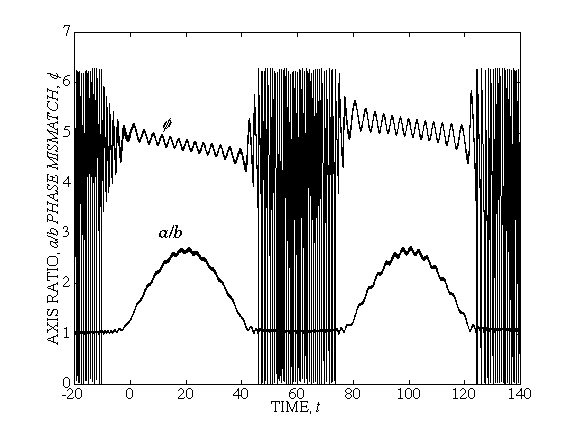
FIGURE on the left shows the evolution of the axis ratio r
and
phase mismatch F=q-f
between the vortex rotation phase and the phase of the driving oscillation
for the case of oscillating frequency
w(t)=w/2+10sin(0.157t)
of the driving flow. One can see repetitive autoresonant excitations during
two periods of oscillations of w. One can also
see the phase locking in the system in the autoresonance stages of evolution.
THE
FIGURE on the left shows the evolution of the axis ratio r
and
phase mismatch F=q-f
between the vortex rotation phase and the phase of the driving oscillation
for the case of oscillating frequency
w(t)=w/2+10sin(0.157t)
of the driving flow. One can see repetitive autoresonant excitations during
two periods of oscillations of w. One can also
see the phase locking in the system in the autoresonance stages of evolution.