Superconducting Josephson circuits: phase qubits and beyond

The information content and resulting computational power of an interacting quantum system can grow exponentially with the number of components. However, the effect of decoherence is to rapidly collapse these complex entangled states onto a much smaller subset of classical, so called "pointer" states [1]. A broad effort within experimental physics is now aimed at studying this quantum-classical interface and pushing the limits of decoherence to make larger quantum systems.

Solid state physics has been slow to plunge into this direction since the required isolation and control, seemed difficult (some said impossible) to achieve. The rapid and multiple decoherence pathways of the condensed matter state were felt to prohibit the fabrication of any ultimately useful devices. Pioneering research into the coherent interference of electrons in semiconductors [6] and studies of macroscopic quantum tunneling in superconductors [7] (just to name two representative examples) led to the realization that controllable multi-particle entangled states are now within reach.

Thus, both conceptual and technical experimental advances, have brought to the fore the emerging field of condensed matter quantum state engineering. Superconducting Josephson [8] and Spintronic [9] devices are now fabricated successfully in many groups worldwide. The precision, scalability and reproducibility of solid-state fabrication bode well for the future of such projects.

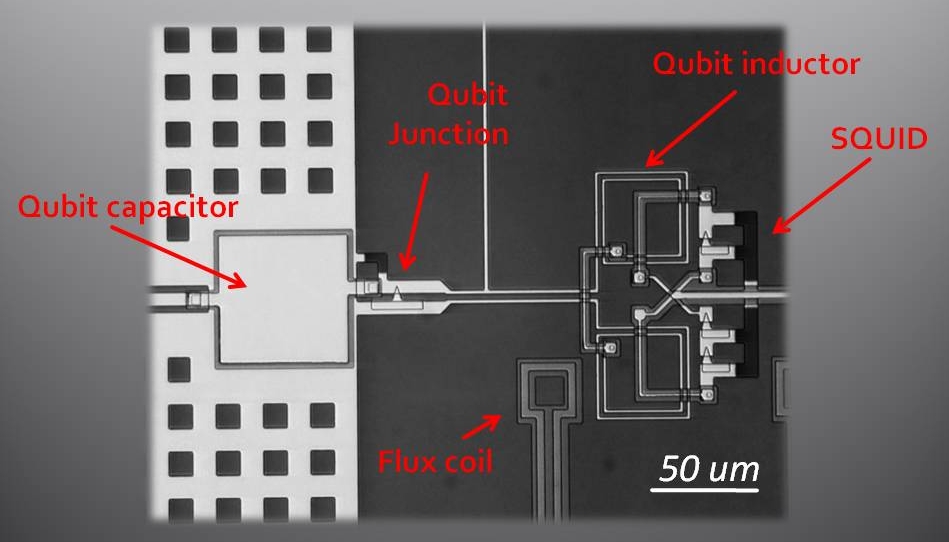Specifically, in recent years a break-though in experimental superconducting quantum circuit fabrication has been achieved [10-13]. These devices are superconducting resonators, including at least one Josephson tunnel barrier element. The Josephson sinusoidal potential (as a function of the superconducting phase change across the junction) supplies the necessary nonlinearity to create identifiable and addressable energy states. Typically in most groups, two such states are singled out and their superposed state is the qubit [14].

The relatively high quality factors (104, closer to 105 for most groups today) and low temperatures (~20 mK) at which the experiments are carried out, bring us deep into the quantum regime. Control bias and microwave pulses (on or off resonance with the ~6 GHz transitions) are used to create and manipulate superposition states.

The phase qubit

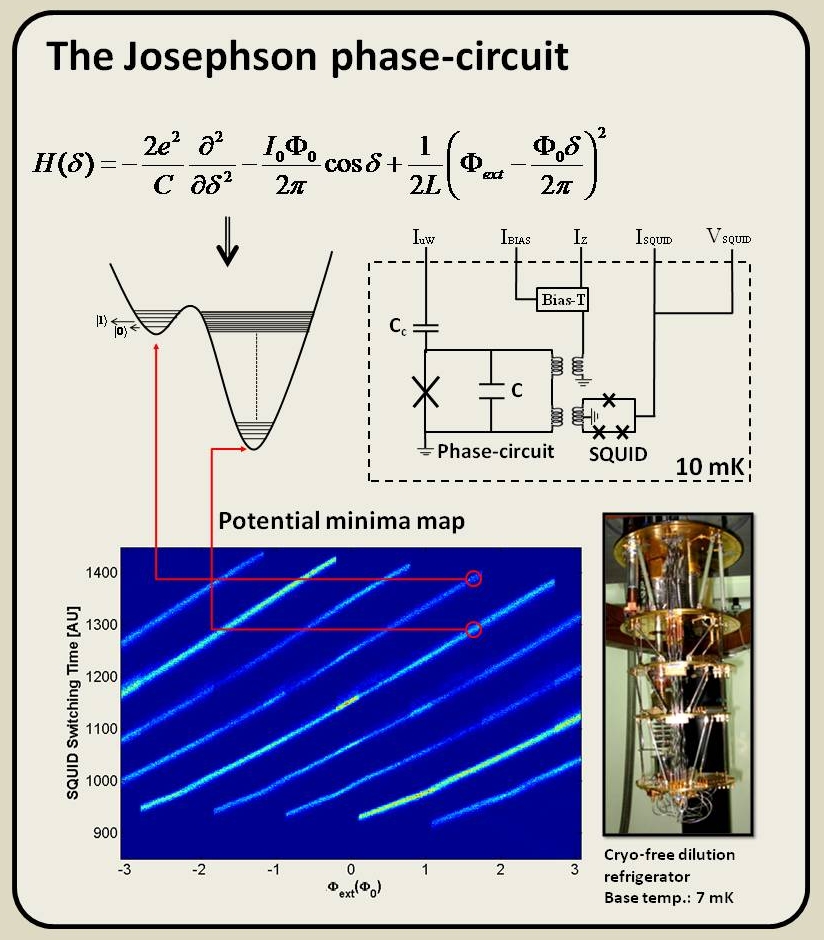Although there is a major interest in multiple qubit fabrication and control, even the single phase qubit is remarkably useful and interesting. The phase qubit stands apart from the other Josephson qubits in that its transition frequency can be tuned over a large range (typically about 2 GHz, which is a 30% relative change), with decoherence remaining manageable throughout. Using this property, the coupling between the macroscopically sized qubit and atomic-sized electronic defect states, both with spectroscopy and in the time domain, has been measured [24].

Interestingly, the phase qubit also has extremely low coupling impedance - about 50 Ohms. This means that it is very easy and natural to couple phase qubits together by simply wiring capacitors or inductors between them. This is a distinctive property, which is markedly different from other qubit systems (both atomic and condensed matter implementations), where the impedance is typically orders of magnitude larger.

An important avenue of decoherence for phase qubits is due to two-level defect states in the surrounding dielectric material [24, 25]. Other Josephson qubits are also affected by the interaction with these defects, but this has not been studied as carefully, to date. This is a fermionic bath, which behaves very differently from the more familiar and well-studied bosonic bath [26]. Very recently several fermionic analogs of the bosonic fluctuation-dissipation theorem have been derived in the theoretical literature [27]. Further experimental evidence for these remarkable connections is needed.

Multi-level quantum systems – qutrits and qudits

Qutrits (three level systems) are of fundamental experimental interest, since they are more robust to certain kinds of decoherence [28] and quantum communication with them is more secure [29]. Also, control of qutrits is an interesting problem, both theoretically and experimentally. Three level systems have been used in atomic physics for demonstrating electromagnetically induced transparency (EIT), stimulated rapid adiabatic passage (STIRAP) and various laser cooling and trapping schemes.

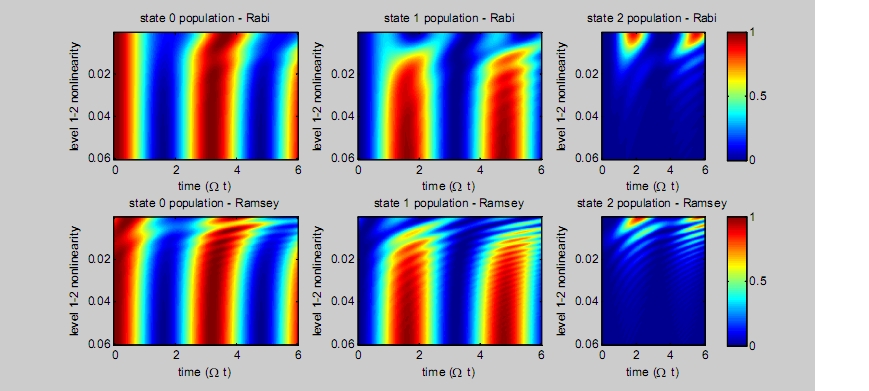Several experiments have been conducted with three quantum levels (or more) in superconducting circuits [30-33]. However, coherence in most of these experiments has been limited, and no systematic benchmarking of the exact states (aside from noting the populations) created was attempted. Often the occupation of additional states outside the qubit manifold was considered an “error” [33] and care was taken to minimize this unwanted leakage of population.

At the quantum coherence lab (at HUJI) we wish to somewhat reverse this viewpoint to try and use these additional states as a resource. We believe that there is a lot to be learnt from both the coherent and incoherent evolution.

Faster gates – higher fidelity

Several theoretical proposals have been brought forward to avoid leakage to unwanted states. A recent experiments have verified that the spectral content of the pulse is indeed critical to lowering such excitation to a tolerable threshold [30].

The next step is to use the external states as stepping stones during manipulation. Properly shaped microwave pulses, with the appropriate phases, can be almost an order of magnitude shorter than the adiabatic pulses of the previous experiments, and if calibrated carefully – can lead to high fidelity gates in the qubit manifold [34].

An exciting possibility is to implement robust analogs of STIRAP in the phase qudits [35]. Multi-tone excitation of the state with precise control of the microwave amplitude and phase is key to success in such schemes.

Tomography revisited

Expanding the dimensionality calls for a larger number of measurements to characterize the state of the system. For example, the density matrix of the qutrit contains eight independent values (vs. three for the qubit). The quadrit (four levels) density matrix contains 15 independent parameters to measure. In general, for a d level system there are d2-1 values to measure.

The phase qubit is especially amenable to multi-level state tomography [36]. The populations can be easily distinguished by altering the measurement pulse amplitude (see Fig. 2). Rotation of the qudit state by microwaves is required for full state tomography. This can be accomplished by careful sideband modulation of a microwave carrier to achieve phase and amplitude consistency throughout in the rotation pulses (which require different frequencies).

Benchmarking the decay of off diagonal components of the nonclassical states created is at the heart of this set of experiments. We are effectively using the qudit as a probe of the environment [37]. Since more phases and transitions are involved, we may be able to get a better handle on the properties of the noise leading to decoherence. Can we observe correlations in the noise spectra? Are multi-photon transitions occurring faster than we expect? There is some preliminary evidence that highly excited states are decaying faster than we expect. It is important to quantify this and especially to check the decay of phase coherences in the system.

© All rights reserved to The Hebrew University of Jerusalem